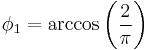Winkel tripel projection
The Winkel Tripel projection (Winkel III), a modified azimuthal map projection, is one of three projections proposed by Oswald Winkel in 1921. The projection is the arithmetic mean of the equirectangular projection and the Aitoff projection:[1] The name Tripel (German for "triple") refers to Winkel's goal of minimizing distortion to the three factors of area, direction or distance.[2]
where  is the longitude from the central meridian of the projection,
is the longitude from the central meridian of the projection,  is the latitude,
is the latitude, 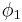 is the standard parallel for the equirectangular projection, and
is the standard parallel for the equirectangular projection, and
 is the unnormalized cardinal sine function (with the discontinuity removed). In his proposal, Winkel set :
is the unnormalized cardinal sine function (with the discontinuity removed). In his proposal, Winkel set :
A closed form inverse mapping does not exist, and computing the inverse numerically is somewhat complicated.
Goldberg and Gott show that the Winkel tripel fares well against several other projections analyzed against their measures of distortion, producing small distance errors, small combinations of Tissot indicatrix ellipticity and area errors, and the smallest skewness of any of the projections they studied.[3] By a different metric, Capek’s “Q”, the Winkel tripel ranked ninth among a hundred map projections of the world, behind the common Eckert IV and Robinson projections.[4]
In 1998, the Winkel Tripel projection replaced the Robinson projection as the standard projection for world maps made by the National Geographic Society. Many educational institutes and textbooks followed National Geographic's example in adopting the projection, and most of those still use it.
References
- ^ Snyder, John P. (1993). Flattening the Earth: Two Thousand Years of Map Projections. Chicago: University of Chicago Press. pp. 231–232. ISBN 0226767477. http://books.google.com/books?id=0UzjTJ4w9yEC&pg=PA282&dq=winkel. Retrieved 2011-11-14.
- ^ "Winkel Tripel Projections". Winkel.org. http://www.winkel.org/other/Winkel%20Tripel%20Projections.htm. Retrieved 2011-11-14.
- ^ Goldberg, David M.; Gott III, J. Richard (2007). "Flexion and Skewness in Map Projections of the Earth". Cartographica 42 (4): 297–318. http://www.physics.drexel.edu/~goldberg/projections/goldberg_gott.pdf. Retrieved 2011-11-14.
- ^ Capek, Richard (2001). "Which is the best projection for the world map?". Proceedings of the 20th International Cartographic Conference (Beijing, China) 5: 3084–93. http://icaci.org/documents/ICC_proceedings/ICC2001/icc2001/file/f24014.doc. Retrieved 2011-11-14.
![x = \frac{1}{2}\left[\lambda \cos(\phi_1) %2B \frac{2 \cos(\phi)\sin\left(\frac{\lambda}{2}\right)}{\mathrm{sinc}(\alpha)}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/efbff5b6cd971155da13a408a6c0836b.png)
![y = \frac{1}{2}\left[\phi %2B \frac{\sin(\phi)}{\mathrm{sinc}(\alpha)}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/d0418e165bf8adb98361aff1d5b46240.png)
![\alpha = \arccos\left[\cos(\phi_1) \cos\left(\frac{\lambda}{2}\right)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/c1120d17836f8186c5440ed99f17a6df.png)